

Ceci est la transcription de l'exposé effectué lors des Journées Perl Francophones 2009. Il y a toutefois un certain nombre de différences avec l'exposé tel qu'il a eu lieu. D'une part, la durée de 40 minutes s'est révélée insuffisante pour évoquer avec un détail suffisant tous les points à traiter (et dire que j'avais envisagé de demander 20 minutes !). D'autre part, compte tenu des remarques et des questions au cours de l'exposé et immédiatement après, certains passages ont été légèrement adaptés. Notamment, j'ai inséré les exemples que j'ai exécutés (et ceux que j'aurai exécutés si j'avais eu le temps) dans une session en ligne de commande.

Source : photo personnelle.
Karl Menninger, Number Words and Number Symbols, A Cultural History of Numbers, Dover Publications, traduction de Zahlwort und Ziffer: Eine Kulturgeschicht der Zahlen.
Geneviève Guitel, Histoire comparée des numérations écrites, éditions Flammarion.
Georges Ifrah, Histoire universelle des chiffres, Seghers, traduit en anglais.Plus Wikipedia, mais seulement pour les images, surtout pas pour le texte.
Notons que Karl Menninger est un linguiste, c'est pourquoi il s'intéresse aux numérations parlées (les mots désignant les nombres) en plus des numérations écrites. Geneviève Guitel et Georges Ifrah sont des mathématiciens et se sont donc intéressés essentiellement aux numérations écrites. D'autre part, dans la suite de l'exposé, je donne les références avec les initiales de l'auteur du livre. Le problème, c'est que cela fait référence à l'exemplaire que j'ai donc, dans le cas de Georges Ifrah, cela fait référence à l'édition de 1981. Or le livre a été réédité dans une version en deux volumes et augmentée. Donc la pagination n'a rien à voir avec celle de 1981. Tant pis !
use Roman;
for my $av (qw/1 5 8 40 84/) {
my $ap = Roman($av);
print "$av -> $ap\n";
}
for my $av (qw/I IV VII XIV LII LXXXIV/) {
my $ap = arabic($av);
print "$av -> $ap\n";
}
use Math::Roman;
for (qw/1 5 8 40 84 I IV VII XIV LII LXXXIV/) {
my $romain = Math::Roman->new($_);
my $arabe = $romain->as_number;
print "$arabe -> $romain\n";
}
use Text::Roman;
for my $av (qw/1 5 8 40 84/) {
my $ap = roman($av);
print "$av -> $ap\n";
}
for my $av (qw/I IV VII XIV LII LXXXIV xiv lii lxxxiv /) {
my $ap = roman2int($av);
print "$av -> $ap\n";
}
J'ai failli passer à côté de ce module, car la proximité de Text et de Roman me faisait penser plutôt à l'encodage ISO-8859-1.
use Convert::Number::Roman;
use utf8;
for my $av (1, 5, 8, 40, 84,
"Ⅰ", "Ⅹ", "ⅬⅢ", "ⅩⅭ",
) {
my $cnr = Convert::Number::Roman->new($av);
my $ap = $cnr->convert;
print "$av -> $ap\n";
}
use Acme::Roman; my $a = LXX; my $b = XIV; print $a + $b, "\n";
Ce module fait lui-même appel à Roman.pm en lui ajoutant une couche de AUTOLOAD, donc certaines des limites de Roman.pm s'appliquent également à Acme::Roman.
Même s'il n'est pas préfixé par Acme, un autre module « pour rigoler » est Lingua::Romana::Perligata par Damian Conway. La version actuelle est 0.50. Exemple :
use Lingua::Romana::Perligata; cumula meis listis III tum IV tum XC tum LX. per quisque nombrum in listis fac sic nombrum tum novumversum egresso scribe. nombrum comementum tum novumversum egresso scribe. cis
Traduction :
use Roman;
push my @list, 3, 4, 90, 60;
foreach $nombr (@list) {
print STDOUT $nombr, "\n";
print STDOUT Roman::Roman($nombr), "\n";
}
(comementum ne signifie pas qu'il faut appeler le module Roman et sa fonction de même nom, mais qu'il faut imprimer la variable en chiffres romains, plutôt qu'en chiffres arabes. J'ai transcrit cela avec l'appel de Roman car le résultat final est le même). Ou un exemple dû à Robin Berjon sur une page que vous connaissez bien :
use Lingua::Romana::Perligata; ao postincresce.
Mark-Jason Dominus a une proposition originale pour les nombres romains. Contrairement à Adriano Ferreira qui a mis à profit AUTOLOAD, M-J D a utilisé tie pour ses exploits.
use Roman;
print "IX + IX = ", $IX + $IX, "\n";
print "XI * IV = ", $XI * $IV, "\n";
print "II ** X = ", $II ** $X, "\n";
print "M - I = ", $M-$I, "\n";
print "Powers of II:\n";
for ($p = $I; $p < $CLVI; $p *= $II) {
print "\t", $p, "\n";
}
Je ne l'ai pas installé sur ma machine.
Je n'ai pas essayé Acme::MetaSyntactic::roman d'Alberto Manuel Brandão Simões et BooK, car son but n'est pas de convertir les nombres romains en valeurs numériques ou réciproquement. De même, je n'ai pas essayé non plus Language::Befunge::IP::lib::ROMA de Jérôme Quelin.
Et il y a sûrement d'autres endroits où l'on pourrait trouver des exemples de conversion de nombres romains. Entre autres, un article de Christian Aperghis-Tramoni sur PIR (à paraître dans Gnu Linux Magazine).
| La numération romaine est basée sur les lettres M, D, C, L, X, V et I. |
| On n'a jamais 4 fois le même symbole à la suite (exception : IIII sur les cadrans d'horloge). |
| La soustraction se fait en mettant un I à gauche d'un V ou d'un X, en mettant un X à gauche d'un L ou d'un C ou un C à gauche d'un D ou d'un M. |
| La soustraction ne peut porter que sur un seul caractère à la fois parmi I, X et C. |
| Le système est additif et soustractif uniquement. |
| Il est impossible de dépasser 3999. |
| La numération romaine est basée sur les lettres M, D, C, L, X, V et I. | FAUX ! |
| On n'a jamais 4 fois le même symbole à la suite (exception : IIII sur les cadrans d'horloge). | FAUX ! |
| La soustraction se fait en mettant un I à gauche d'un V ou d'un X, en mettant un X à gauche d'un L ou d'un C ou un C à gauche d'un D ou d'un M. | FAUX ! |
| La soustraction ne peut porter que sur un seul caractère à la fois parmi I, X et C. | FAUX ! |
| Le système est additif et soustractif uniquement. | FAUX ! |
| Il est impossible de dépasser 3999. | FAUX ! |
Je tempère les affirmations péremptoires ci-dessus. En fait, ces règles correspondent au système simplifié de numération romaine utilisé depuis le XXe siècle. Mais dans la période qui précède, depuis la République romaine jusqu'au XIXe siècle, on trouve des contre-exemples pour chacune de ces règles.

Source : Wikipedia, image dans le domaine public.
Dans les inscriptions archaïques, on trouve d'autres graphies pour L (via Popilia) et pour D que celles auxquelles nous sommes habitués. L'hypothèse soutenue par KM 242 et GI 144 est que cela vient de la pratique de l'entaille par les bergers : pour compter le nombre de moutons dans un troupeau, les bergers prennent un bâton et y inscrivent une encoche pour chaque mouton. Pour mieux lire le nombre résultant, les encoches correspondant à 5, 15, 25, etc. ont une forme différente et les encoches correspondant à 10, 20, 30, etc. ont une autre forme encore. Et on a encore d'autres variantes pour 50 et 100. C'est par la suite que les caractères obtenus ont été assimilés à des lettres. GI 139 indique que les plus anciens exemples d'utilisation de lettres pour les nombres romains remontent au Ier siècle av-J.C.
Selon KM 243, le symbole de 50 viendrait du découpage du symbole primitif de 100 en deux moitiés. Puis le symbole a évolué vers le « L » bien connu. Voici l'évolution pour 50 et 100 :
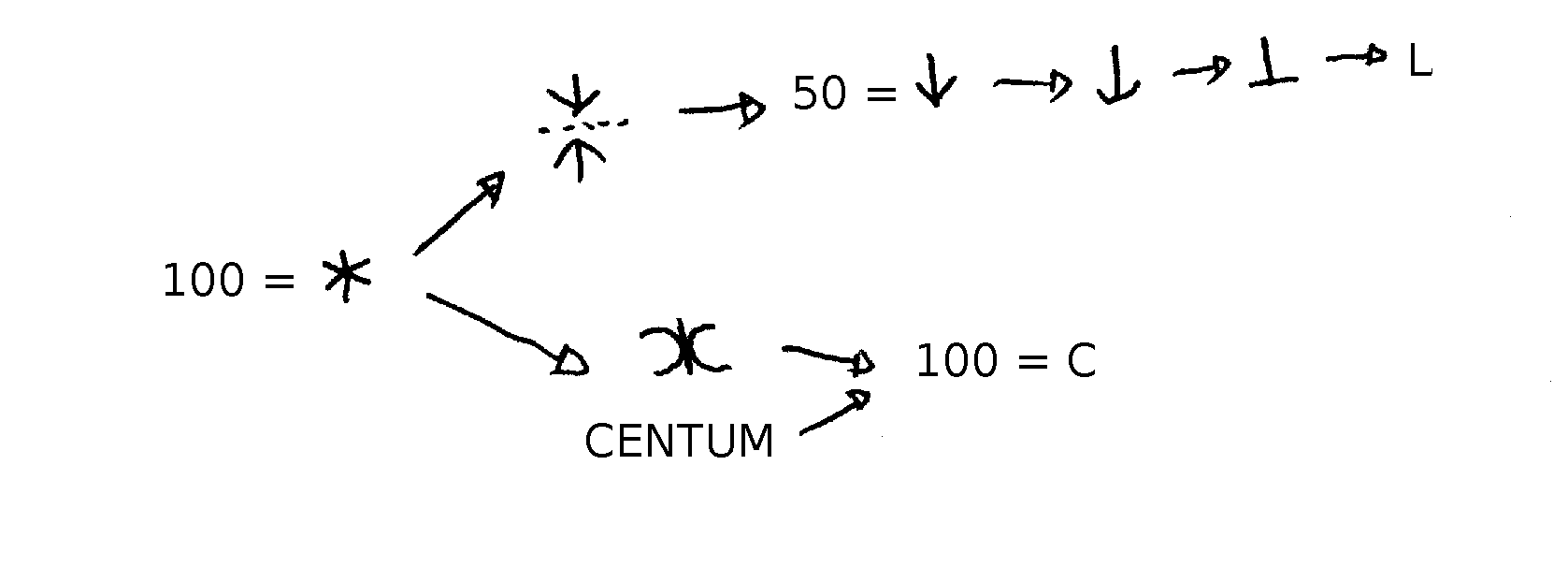
Source : dessin personnel, inspiré de KM 243 et GI 158.
Pour mémoire, KM 243 cite une hypothèse de Mommsen, à laquelle il ne croit pas. L'alphabet étrusque (puis romain) provient de l'alphabet grec, mais certaines lettres comme Ψ et Θ n'ont pas été reprises dans cet alphabet étrusque. Mommsen suppose donc que les Étrusques ont adopté ces deux lettres délaissées pour en faire des chiffres. GG 204 rapporte une hypothèse similaire de J. Marouzeau sans réellement la soutenir.




La plaque date de 260 av J.C, il y a donc douze siècles. Comme le lapicide ayant gravé cette plaque est mort depuis plus de 70 ans, cette plaque est dans le domaine public. Quant à Spinoza et Descartes, ils ont vécu au XVIIe siècle, donc là aussi leurs livres sont dans le domaine public. Sources : Glossographia de Stephen Chrisomalis pour la plaque de la colonne rostrale et Commons Wikimedia. pour les pages de garde.
Pour 1 000, la graphie archaïque est « (|) » (ou « ↀ », ou « ⅽⅠↃ ») et pour D, c'est |) » (ou « ⅠↃ »), que l'on peut voir dès la colonne rostrale de Duilius et qui a longtemps survécu (pages de garde de Descartes et de Spinoza). On a également une autre graphie pour M, un « noeud papillon » ∞ qui, d'après KM 245, a été repris par Wallis pour désigner l'infini.
D'où la justification du Consortium Unicode de déclarer des codepoints spécifiques pour ces caractères.
| 2160 | Ⅰ | 2168 | Ⅸ | 2170 | ⅰ | 2178 | ⅸ | 2180 | ↀ |
| 2161 | Ⅱ | 2169 | Ⅹ | 2171 | ⅱ | 2179 | ⅹ | 2181 | ↁ |
| 2162 | Ⅲ | 216A | Ⅺ | 2172 | ⅲ | 217A | ⅺ | 2182 | ↂ |
| 2163 | Ⅳ | 216B | Ⅻ | 2173 | ⅳ | 217B | ⅻ | 2183 | Ↄ |
| 2164 | Ⅴ | 216C | Ⅼ | 2174 | ⅴ | 217C | ⅼ | ||
| 2165 | Ⅵ | 216D | Ⅽ | 2175 | ⅵ | 217D | ⅽ | ||
| 2166 | Ⅶ | 216E | Ⅾ | 2176 | ⅶ | 217E | ⅾ | ||
| 2167 | Ⅷ | 216F | Ⅿ | 2177 | ⅷ | 216F | ⅿ |
Problèmes : pourquoi ont-ils éprouvé le besoin de déclarer II, III, IV, VI, VII, VIII, IX, XI et XII ? Pourquoi se sont-ils arrêtés à 12 ? Que donneront VII, VIII et XII dans une police à espacement fixe ?
7 = Ⅶ, 8 = Ⅷ, 12 = Ⅻ
Pourquoi ont-ils utilisé le même codepoint pour le C de 100 et pour le C de « ⅽⅠↃ » ? Pourquoi ont-ils utilisé le même codepoint pour le I de 1 et pour le | de « ⅽⅠↃ » ?
Roman, Math::Roman et Text::Roman ne digèrent pas Unicode.
Convert::Number::Roman ne digère QUE Unicode (aviez-vous remarqué le use utf8 dans l'exemple ci-dessus ?). Mais il n'admet pas « (|) », que ce soit sous la forme "\x{2180}" (« ↀ ») ou sous la forme "\x{216D}\x{2160}\x{2183}" (« ⅽⅠↃ »). En fait, Convert::Number::Roman est une implémentation fidèle de http://www.w3.org/TR/css3-lists/ qui requiert l'utilisation de la plage U+2160 -> U+2183 mais ignore U+0043 (« C »), U+0044 (« D ») etc. D'autre part, pour le nombre 1000, cette spécification évoque uniquement U+216F (« M ») et non U+2180 (« ↀ ») ou la combinaison U+216D,U+2160,U+2183 (« ⅽⅠↃ »).
Lorsque sont apparues les lettres minuscules au Moyen-Âge, elles ont été utilisées également pour écrire les chiffres romains. Dans certains cas, pour faire joli ou pour prévenir les escroqueries, le « i » final est remplacé par un « j ». Le Consortium Unicode n'a pas voulu créer un code-point pour « j », sans doute ont-ils considéré que c'était un glyphe différent pour le même caractère (rappelons que les variations de glyphes pour un même caractère sont en dehors du champ d'Unicode ; cf. les glyphes initiaux, médians, finaux et isolés des caractères arabes).
Les Romains ont utilisé le « S » pour la fraction 1/2, la seule qu'ils aient utilisée. À noter qu'un sesterce vaut 2,5 as, donc l'abréviation du sesterce HS provient en réalité de IIS(barré). Étymologiquement, « sesterce » signifie « presque trois », c'est-à-dire « 3 - 0,5 ». KM 160-285 signale également un I avec une petite barre oblique pour 0,5, un V avec une petite barre oblique pour 4,5 et un X avec une petite barre oblique pour 9,5. Le Consortium Unicode n'a rien prévu pour le S, le I barré, le V barré et le X barré.
Aucun des quatre modules « sérieux » ne digère le S. Roman, Text::Roman et Convert::Number::Roman acceptent les minuscules (U+2170 à U+217F pour Convert::Number::Roman) mais pas Math::Roman. Roman, Math::Roman et Text::Roman refusent le « j ». Pour Convert::Number::Roman, comme je l'ai déjà dit pour Unicode, cela peut être considéré comme une question de variation de glyphe, donc indépendant du module.

Source : Wikipedia. Image dans le domaine public.
Dans la stèle de la Via Popilia, on trouve le nombre 74 écrit sous la forme « LXXIIII » (distance de Muranum) et le nombre 917 sous la forme « DCCCCXVII ». D'autre part, si vous visitez le château de Boury-en-Vexin (dans l'Oise à la limite de l'Eure près de Gisors), vous pourrez remarquer une plaque tombale qui porte la date 1844 sous la forme « MDCCCXXXXIV ».
L'utilisation d'un symbole quadruple est loin d'être une exception à la règle du principe soustractif. GI 142 va même jusqu'à dire que le principe soustractif « fut assez limité sur les inscriptions soignées ».
La seule survivance actuelle de cette pratique est le « 4 d'horloger », que l'on trouve sur les cadrans de pendules et d'horloges. Notons toutefois que certains cadrans d'horloge assez anciens utilisent « VIIII » pour « 9 » et, dans le cas de cadrans à 24 heures, « XIIII » pour 14, « XVIIII » pour 19 et « XXIIII » pour 24.


Source : photos personelles d'Yves Agostini, transmises après l'exposé. License Creative Commons « BY ».
Roman, Math::Roman et Text::Roman refusent un symbole quadruple. Convert::Number::Roman accepte un « X » quadruple, un « C » quadruple ou un « M » quadruple. Il accepte même le quintuplement (testé pour « C »). Quant au quadruplement de « I », comme je l'ai déjà dit dans le cas du « j », on peut considérer que « IIII » est une variation de glyphe pour U+2163 = « IV ».
GG 226 cite la date de parution d'un ouvrage, qui a été publié à Leyde en 1599, soit « ⅽⅠↃ ⅠↃ Ⅰⅽ ». Donc, on admet la soustraction de I à C. Cela dit, il ne s'agit peut-être pas d'une règle générale et GG justifie cette entorse (si tant est que c'est une entorse) par le fait que le résultat est typographiquement élégant.


Sources : Via Popilia, Wikipedia, image dans le domaine public. Cent Emblemes Chrestiens université de Glasgow, livre également dans le domaine public, Georgette de Montenay étant décédée en 1581.
Retour à la Via Popilia, encore une fois. Le lapicide a eu des problèmes de longueur de ligne lorsqu'il a gravé la distance jusqu'à Reggio de Calabre, pour écrire 321 sous la forme « CCCXXI ». Il avait déjà eu un problème avec la distance de 84 milles jusqu'à Capoue, mais il s'en était sorti en exprimant cette distance sous la forme « XXCIIII », plus compacte que « LXXXIV ». On retrouve la même expression de 84 sur la page de garde d'un livre de Georgette de Montenay, publié en 1584, soit « ⅽⅠↃ. ⅠↃ. XXCIIII. ». Et là, on ne peut pas dire que l'imprimeur était limité par la largeur de la feuille de papier. Beaucoup plus récent, il y a le « Palm IIIx », que certains appellent « Palm 7 ». Finalement, il y a un paragraphe sur la page de Wikipedia sur les extensions modernes des nombres romains, mais j'ai des doutes énormes sur la véracité des mécanismes qui y sont décrits.
Remarque : pour trouver des pages intéressantes sur les nombres romains sur Google, il ne faut pas chercher « nombres romains » mais « XXCIIII ». C'est ainsi que j'ai découvert la page de garde du livre de Georgette de Montenay. Et j'y ai trouvé également la page sur la numération de romaine de la wikipedia... norvégienne.
Roman, Math::Roman et Text::Roman refusent une soustraction double. Convert::Number::Roman l'admet, mais renvoie un mauvais résultat.
À partir du Moyen-Âge, on trouve un mécanisme multiplicatif. Cela dit, KM 281 signale que sous l'Empire romain, on avait occasionnellement « IIM » pour 2 000. Mais la plupart des exemples que j'ai trouvés dans les trois livres et ailleurs indiquent une date au Moyen-Âge ou postérieure. Voici les différents exemples réunis par KM et GG.
88 IIIIxx et huit KM 285 GG 225 texte de 1388
M C
4473 florins IIII, IIII, LXXIII GG 225, manuscrit espagnol de 1392
451 234 678 567 four Cli, two Cxxxiiii, millions, sixe Clxxviii M. five Clxvii
GG 225 texte de Baker en 1568
300 000 CCCM KM 285, texte de 1550
M C
1859 Gulden I viij lix Gulden KM 285, livre de compte de Rüsselheim
C
1859 Gulden xviii lix Gulden KM 285, une autre partie du livre de compte de Rüsselheim
c
1612 MVI XII KM 285, texte de Köbel
c xx
1485 mil.IIII IIII et V KM 285
E c
25/06/1644 XXV. IVIN M.VI.XLIIII église de Saint-Crépin-Ibouvillers (visite personnelle)
Et pour en revenir au Palm IIIx, compte tenu de la différence
de typographie entre les « I » et le « x »,
j'aurais personnellement tendance à interpréter cela comme
une multiplication et donc à traduire en « Palm 30 ».
Pas testé, je ne sais pas comment représenter la juxtaposition verticale de deux symboles ou le positionnement vertical d'une lettre au-dessus de la ligne.
Lorsque l'on a autre chose à compter que des pages de préface, des chapitres et des dynasties, lorsque l'on recense les habitants et que l'on collecte des impôts, on dépasse facilement 3999. N'en déplaise à Adriano Ferreira qui dit, dans le POD de son module,
Acme::Roman does not like numbers greater than 3999. Why would you like such big numbers?(Comme il s'agit d'un module Acme::, il y a de fortes chances que l'auteur ne soit pas complètement sérieux dans le POD.) On a déjà vu ci-dessus comment, au Moyen-Âge, la notation multiplicative permettait de dépasser 3999, mais même en se contentant de la notation additive et éventuellement soustractive, les Romains dépassaient allègrement 3999.

Source : Glossographia de Stephen Chrisomalis, image dans le domaine public.
J'ai déjà exposé le symbole pour 1000, U+2180 ou ↀ. Il existe aussi un symbole pour 5 000, U+2181 ou ↁ ou encore ainsi qu'un symbole pour 10 000, U+2182 ou ↂ. Mais ce que le Consortium Unicode a oublié, c'est que les Romains continuaient avec 50 000 = « |))) » = « ⅠↃↃↃ » et 100 000 = « (((|))) » = « ⅽⅽⅽⅠↃↃↃ ». Et il n'y a donc pas de caractère Unicode pour ces deux nombres. GI 339 a relevé 13 stylisations différentes en plus du graphisme de base. En voici quelques-uns :
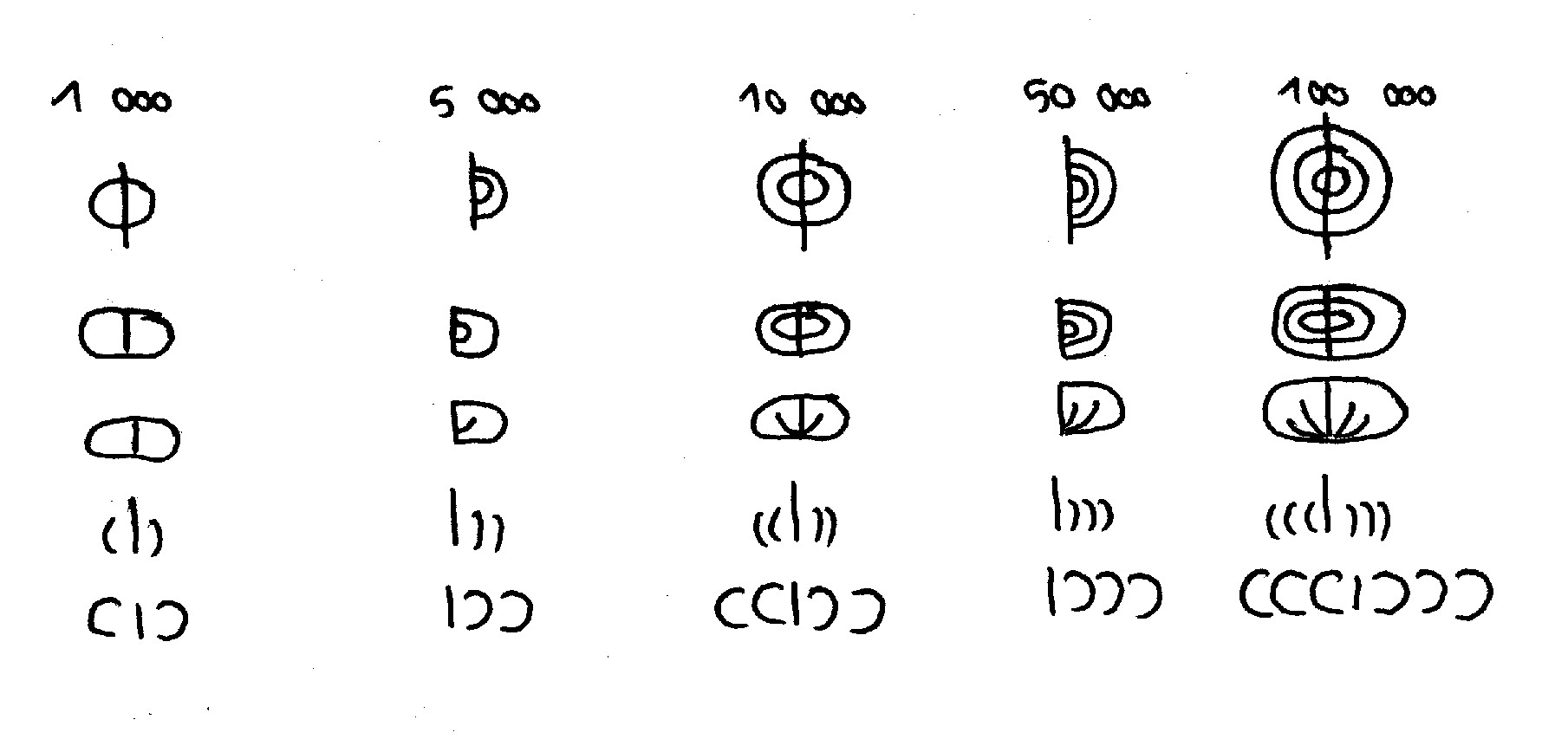
Source : dessin personnel, inspiré de GI 339.
En revanche, on ne va pas plus loin que 100 000. Ainsi, pour
exprimer un butin dépassant les 2 millions de pièces de bronze,
la colonne rostrale de Duilius comporte entre 23 et 33 fois le caractère
![]() « ⅽⅽⅽⅠↃↃↃ »
(selon les estimations de GI 340).
C'est le plus grand nombre écrit « en chiffres ».
Mais les Romains pouvaient encore aller un peu plus loin.
KM 44 et GG 208 rappellent que la dette publique à l'avènement de
Vespasien était de 40 milliards de sesterces et que Suétone l'a
écrit dans son Histoire des Césars.
À noter que KM 28 dit que c'est le trésor impérial, pas la dette publique.
« ⅽⅽⅽⅠↃↃↃ »
(selon les estimations de GI 340).
C'est le plus grand nombre écrit « en chiffres ».
Mais les Romains pouvaient encore aller un peu plus loin.
KM 44 et GG 208 rappellent que la dette publique à l'avènement de
Vespasien était de 40 milliards de sesterces et que Suétone l'a
écrit dans son Histoire des Césars.
À noter que KM 28 dit que c'est le trésor impérial, pas la dette publique.
Convert::Number::Roman sait interprêter U+2181 = ↁ = 5 000 ainsi que U+2182 = ↂ = 10 000, mais il s'arrête là, comme Unicode et il ne sait pas traiter la composition de U+216D, U+2160 et U+2183 pour ces mêmes nombres ni pour 50 000 et 100 000. Lingua::Romana::Perligata sait afficher de tels nombres. Exemple :
use Lingua::Romana::Perligata; nombro II tum XVI elevamentum da. nombrum tum novumversum egresso scribe. nombrum comementum tum novumversum egresso scribe.donne :
65536 I)))((I))I))DXXXVIJe n'ai pas réussi à écrire un script où Lingua::Romana::Perligata lit un tel nombre. D'où le fait que je soit passé par l'opération 2**16 pour alimenter la variable $nombr ci-dessus. Aucun autre module ne sait traiter ces nombres.
Chez les Romains, le seuil pour les très grands nombres était 100 000, tout comme c'est le milliard pour nous : nous changeons de mode d'expression à partir du billion et nous adoptons la notation avec les puissances de 10. De même, chez les Romains, le mécanisme de base de la numération va jusqu'à 100 000. D'ailleurs, le mot million n'existe pas en latin antique (par opposition à celui utilisé au Moyen-Âge) et ce mot n'apparaît qu'en 1359 en France (GG 205 KM 143, mais GG 567 donne la date de 1270). Cela dit, trois farfelus sont passés outre cette limite.
En 1582 Freigius utilise ⅽⅽⅽⅽ|ↃↃↃↃ pour le million et |ↃↃↃↃ pour 500 000 (GG 212, GI 338-343).
En décembre 2000, Damian Conway publie Lingua::Romana::Perligata où il exprime 9 999 999 999 sous la forme (((((((I)))))))((((((((I))))))))((((((I))))))(((((((I)))))))(((((I)))))((((((I))))))((((I))))(((((I)))))(((I)))((((I))))((I))(((I)))M((I))CMXCIX
En juin 2009, Jean Forget présente un exposé sur les nombres romains où il écrit le nombre d'Avogadro 6E+23 sous la forme |))))))))))))))))))))))(((((((((((((((((((((|))))))))))))))))))))) et le googol 1+E100 sous la forme ((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((|))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))
Remarque : on est encore loin d'Archimède et de son Arénaire, ainsi que des prouesses des savants hindous.
Autre remarque : j'ai tapé la totalité de ce texte sous Emacs, à l'exception du paragraphe précédent, pour lequel j'ai utilisé Vi. Voici comment taper un googol en chiffres romains en moins de 10 secondes sans se tromper (ne tapez pas les espaces, il sont là pour faciliter la lisibilité) :
98 a ( <Esc> a | <Esc> 98 a ) <Esc>Attention, il faut parfois utiliser les chiffres de la rangée supérieure du clavier, le pavé numérique ne donnant pas le résultat escompté.
Une autre façon d'exprimer les grands nombres en chiffres romains consiste à utiliser le surlignement, qui multiplie par 1 000. Et pour multiplier par 100 000, on utilise un « portail », une boîte rectangulaire réduite à trois côtés en supprimant le côté inférieur. Exemples :
-------
83 000 LXXXIII GI 339
----
4 870 IIIIDDCCLXX GI 340
-----
1 200 000 |XII| GI 342
------
1 300 000 |XIII| GI 342
----
200 000 000 |ↀↀ| GI 342
- ------
164 351 c.lxiiij.ccc.l.i GG 225, Adélard de Bath 1120
Cela dit, les auteurs divergent légèrement à ce sujet. KM 245-281 signale que cette méthode s'observe essentiellement au Moyen-Âge, pas sous l'Empire Romain. Sous l'Empire Romain, le surlignement des chiffres sert à différentier les lettres-chiffres des vraies lettres. Exemples :
---
IIIVIR = triumvir (KM 281, GI 340)
---
COMMENT PARTAGER DIX CACAHUÈTES ENTRE DIX PERSONNES (exemple inventé)
Comment partager 509 cacahuètes entre 10 personnes.
GI 340 note l'existence de ce système (le surlignement pour marquer un contexte numérique), mais pour lui, c'est un usage très ancien. Dès la fin de la République romaine, le surlignement servait à multiplier par 1000. On peut noter que le surlignement et le portail ne sont pas antinomiques avec la symbolique ↀ, ces deux symboliques sont utilisées sur un abaque romain conservé au Cabinet des Médailles de la Bibliothèque Nationale de Paris. Sur cet abaque, les en-têtes des sept colonnes de gauche sont :
--- |X| (((|))) ((|)) ∞ C X I
(Les colonnes de droite concernent les sous-multiples du sesterce. Lire KM ou GI pour plus de détails.)

Source : Wikipedia photo sous Licence de documentation libre GNU.
KM 28, GG 223 et GI 343 rapportent une anecdote contée par Suétone dans son Histoire des Césars. Dans son testament, Livie avait légué à Galba la somme de :
------- HS 'CCCCC'(Remarquez la longueur réduite des pans verticaux du portail.) Galba espérait donc empocher 50 millions de sesterces,
------- HS |CCCCC|(CCCCC dans un « portail »). Mais Tibère a décrété que le testament portait sur 500 000 sesterces, c'est-à-dire :
----- HS CCCCCles traits descendants étant, prétendait-il, trop petits pour avoir une signification. À noter que dans la version de KM 28, Galba a reçu juste 500 sesterces, le surlignement étant, selon KM, rarement une marque de multiplication par 1000.
GI 341 note qu'il n'existe aucun témoignage probant pour un éventuel double surlignement qui aurait multiplié par un million. Cela s'explique par le fait que les Romains plaçaient leur seuil des grands nombres à 100 000 et non pas à 1 000 000 (GG 213-218). Cela n'a pas empêché Wikipedia de prétendre que les millions utilisent un double-macron. Cela n'a pas empêché non plus le W3C de spécifier l'utilisation d'un surlignement double, puis triple, puis quadruple et ainsi de suite pour les millions, les milliards et la suite. Cf. la spécification sur les listes HTML. Voici un exemple de liste obtenu avec :
<ol start='123456789' type='I'>Si votre navigateur HTML est suffisamment récent, vous verrez des chiffres romains avec des surlignements. Sur ma machine, ce n'est pas le cas.
Convert::Number::Roman pratique le surlignement simple (c'est bien) et le double surlignement ou triple ou plus (c'est mal, mais c'est cohérent avec http://www.w3.org/TR/css3-lists/). Il ne connaît pas le portail (Unicode et le W3C non plus). Et il sait convertir dans l'autre sens. Voici un exemple. Notons que lorsque je l'exécute sur une console, les surlignements sont bien combinés avec les caractères précédents. Mais à l'affichage sur Firefox, les surlignements sont parfois juxtaposés. Vous aurez peut-être un résultat différent en fonction du programme utilisé et même de sa version.
#!/usr/bin/perl
#
# Tests sur les modules de nombres romains
#
use strict;
use warnings;
use Convert::Number::Roman;
use charnames ':full';
for my $av (1, 5, 7, 8, 12, 13, 40, 84, 1024, 8192, 65536, 1048576, 2130706433,
) {
my $cnr = Convert::Number::Roman->new($av);
my $ap = $cnr->convert;
my $cnr1 = Convert::Number::Roman->new($ap);
my $av1 = $cnr1->convert;
print "$av -> $ap -> $av1\n";
#print "$av -> ", join '', map { sprintf "&#%d;", ord($_) } split '', $ap;
#print " -> $av1\n";
foreach (split '', $ap) {
printf " U+%04X %s\n", ord($_), charnames::viacode(ord($_));
}
}
1 -> Ⅰ -> 1
U+2160 ROMAN NUMERAL ONE
5 -> Ⅴ -> 5
U+2164 ROMAN NUMERAL FIVE
7 -> Ⅶ -> 7
U+2166 ROMAN NUMERAL SEVEN
8 -> Ⅷ -> 8
U+2167 ROMAN NUMERAL EIGHT
12 -> Ⅻ -> 12
U+216B ROMAN NUMERAL TWELVE
13 -> ⅩⅢ -> 13
U+2169 ROMAN NUMERAL TEN
U+2162 ROMAN NUMERAL THREE
40 -> ⅩⅬ -> 40
U+2169 ROMAN NUMERAL TEN
U+216C ROMAN NUMERAL FIFTY
84 -> ⅬⅩⅩⅩⅣ -> 84
U+216C ROMAN NUMERAL FIFTY
U+2169 ROMAN NUMERAL TEN
U+2169 ROMAN NUMERAL TEN
U+2169 ROMAN NUMERAL TEN
U+2163 ROMAN NUMERAL FOUR
1024 -> ⅯⅩⅩⅣ -> 1024
U+216F ROMAN NUMERAL ONE THOUSAND
U+2169 ROMAN NUMERAL TEN
U+2169 ROMAN NUMERAL TEN
U+2163 ROMAN NUMERAL FOUR
8192 -> ↁⅯⅯⅯⅭⅩⅭⅡ -> 8192
U+2181 ROMAN NUMERAL FIVE THOUSAND
U+216F ROMAN NUMERAL ONE THOUSAND
U+216F ROMAN NUMERAL ONE THOUSAND
U+216F ROMAN NUMERAL ONE THOUSAND
U+216D ROMAN NUMERAL ONE HUNDRED
U+2169 ROMAN NUMERAL TEN
U+216D ROMAN NUMERAL ONE HUNDRED
U+2161 ROMAN NUMERAL TWO
65536 -> Ⅼ̄Ⅹ̄Ⅴ̄ⅮⅩⅩⅩⅥ -> 65536
U+216C ROMAN NUMERAL FIFTY
U+0304 COMBINING MACRON
U+2169 ROMAN NUMERAL TEN
U+0304 COMBINING MACRON
U+2164 ROMAN NUMERAL FIVE
U+0304 COMBINING MACRON
U+216E ROMAN NUMERAL FIVE HUNDRED
U+2169 ROMAN NUMERAL TEN
U+2169 ROMAN NUMERAL TEN
U+2169 ROMAN NUMERAL TEN
U+2165 ROMAN NUMERAL SIX
1048576 -> Ⅰ̿Ⅹ̄Ⅼ̄Ⅷ̄ⅮⅬⅩⅩⅥ -> 1048576
U+2160 ROMAN NUMERAL ONE
U+033F COMBINING DOUBLE OVERLINE
U+2169 ROMAN NUMERAL TEN
U+0304 COMBINING MACRON
U+216C ROMAN NUMERAL FIFTY
U+0304 COMBINING MACRON
U+2167 ROMAN NUMERAL EIGHT
U+0304 COMBINING MACRON
U+216E ROMAN NUMERAL FIVE HUNDRED
U+216C ROMAN NUMERAL FIFTY
U+2169 ROMAN NUMERAL TEN
U+2169 ROMAN NUMERAL TEN
U+2165 ROMAN NUMERAL SIX
2130706433 -> Ⅱ̿̄Ⅽ̿Ⅹ̿Ⅹ̿Ⅹ̿Ⅾ̄Ⅽ̄Ⅽ̄Ⅵ̄ⅭⅮⅩⅩⅩⅢ -> 2130706433
U+2161 ROMAN NUMERAL TWO
U+033F COMBINING DOUBLE OVERLINE
U+0304 COMBINING MACRON
U+216D ROMAN NUMERAL ONE HUNDRED
U+033F COMBINING DOUBLE OVERLINE
U+2169 ROMAN NUMERAL TEN
U+033F COMBINING DOUBLE OVERLINE
U+2169 ROMAN NUMERAL TEN
U+033F COMBINING DOUBLE OVERLINE
U+2169 ROMAN NUMERAL TEN
U+033F COMBINING DOUBLE OVERLINE
U+216E ROMAN NUMERAL FIVE HUNDRED
U+0304 COMBINING MACRON
U+216D ROMAN NUMERAL ONE HUNDRED
U+0304 COMBINING MACRON
U+216D ROMAN NUMERAL ONE HUNDRED
U+0304 COMBINING MACRON
U+2165 ROMAN NUMERAL SIX
U+0304 COMBINING MACRON
U+216D ROMAN NUMERAL ONE HUNDRED
U+216E ROMAN NUMERAL FIVE HUNDRED
U+2169 ROMAN NUMERAL TEN
U+2169 ROMAN NUMERAL TEN
U+2169 ROMAN NUMERAL TEN
U+2162 ROMAN NUMERAL THREE
Text::Roman remplace le surlignement par l'adjonction d'un blanc souligné (U+005F) ou plusieurs et sait lire les nombres ainsi exprimés, par exemple "LX_XXIII" qui vaut 60 023. Cela dit, il faut changer de fonction pour lire les nombres comportant une marque de multiplication par 1000. Ansi :
use Text::Roman;
for my $av (qw/I IV LX_XXIII L_X_XXIII/) {
my $ap = roman2int($av);
print "roman2int $av -> $ap\n";
$ap = mroman2int($av);
print "mroman2int $av -> $ap\n";
}
produira :
roman2int I -> 1 mroman2int I -> roman2int IV -> 4 mroman2int IV -> roman2int LX_XXIII -> mroman2int LX_XXIII -> 60023 roman2int L_X_XXIII -> mroman2int L_X_XXIII -> 60023Le « m » initial de mroman2int signifie « milhar » et désigne selon Peter de Padua Krauss les nombres romains avec un surligné multipliant par 1000. Il semblerait que ce soit un mot directement importé du portugais C'est pour cela que j'ai accusé Peter de Padua Krauss, un brésilien selon son adresse électronique plutôt que Stanislas Pusep. D'autre part, l'auteur commet une erreur en prétendant que les nombres romains « milhar » peuvent aller jusqu'à 4 002 999. Ce nombre est obtenu à partir de la formule 3999 x 1000 + 3999, en laissant supposer que l'on peut trouver dans un même nombre des « M » simples et des « I » surlignés. C'est faux.
Aucun autre module ne traite le surlignement.
L'adresse IP de ma machine est 2 130 706 433. Mais on a l'habitude de l'exprimer autrement avec une notation pointée : 127.0.0.1, avec des facteurs 16 277 216, 65 536, 256 et 1. Un mécanisme analogue existe pour les chiffres romains, mais avec des facteurs 100 000, 1 000 et 1. Exemples :
312 600 III.XII.DC GG 216 citant l'Encyclopédie de B. Dupiney de Vorepierre 1 250 500 XII.L.D GG 216 citant Alpinolo Natucci
Mais il existe des irrégularités, abondamment discutées par GG. En effet, le point peut effectuer une multiplication par 1 000 ou par 100 000, mais il peut aussi simplement marquer l'addition par concaténation. Dans certains cas, il est possible de reconstituer le rôle exact de chaque point, dans d'autres cas plusieurs solutions sont possibles. Par exemple,
XVII.L. valant au choix 17 050, 1 700 050 ou 1 750 000 GG 218 II.DCCC.XIIII valant forcément 2 814 GG 225

Source : Wikipedia photo sous Licence de documentation libre GNU.
Programmer avec X-Windows, c'est comme extraire la racine carrée de π en utilisant des chiffres romains.
Citation anonyme trouvée dans Unix Haters
Si l'on en croit Wikipedia, pour calculer, les Romains étaient amenés à apprendre des résultats par coeur, comme par exemple XII x XII = CXLIV, ce qui permettrait d'en déduire le produit de XII par un de plus ou un de moins. Mais ce n'est pas en connaissant par coeur le carré de 12 que l'on saura calculer 720 x 62. Il est vrai que l'auteur de ce paragraphe commence sa phrase par « Il se peut que » pour signaler que ce n'est qu'une supposition de sa part. En réalité, le mode de calcul est relativement bien connu et il est décrit dans le chapitre 8 de GI et les pages 297 à 388 de KM (mais pas seulement pour les Romains). Les Romains utilisaient des abaques (« tables à poussières » ou autres variétés). Il s'agit en fait d'une numérotation positionnelle, mais inadaptée à la conservation des nombres. En d'autres termes, ils n'ont pas su, ou pas pensé, à implémenter la persistance dans les abaques.
L'abaque permet de faire les quatre opérations, mais guère plus (quoique Richard Feynman rapporte sa rencontre avec un Japonais qui extrayait des racines cubiques sur un boulier, dont le mode de fonctionnement est similaire à celui de l'abaque ci-dessus). Comment faire des calculs plus compliqués ? Comment, par exemple, trouver la racine carrée de π ? Ce n'est pas dit dans KM, GG et GI, mais il est vraisemblable que les Romains qui avaient besoin de calculs plus compliqués, c'est-à-dire les scientifiques (rares) et les ingénieurs (quand même plus nombreux) avaient reçu une éducation plus poussée que la grande moyenne de leurs concitoyens. Cette éducation comportait l'apprentissage de la langue grecque (lue, écrite, parlée). Donc les scientifiques et les ingénieurs pouvaient apprendre la numération grecque et les méthodes de calcul de leurs prédécesseurs grecs : Euclide, Thales, Eratosthène, Archimède, etc.
Le système simplifié de numération romaine, celui que tout le monde connaît, est bien couvert par trois modules simples et peu encombrants : Roman, Text::Roman et Math::Roman. À vous de choisir lequel possède l'API qui vous convient le mieux. Ce n'est pas comme d'autres domaines où les modules sont légions et de qualité hautement variable : courrier électronique, programmation orientée objet, etc. Quant au quatrième, Convert::Number::Roman, le seul pour l'instant qui sait traiter Unicode, on ne peut que regretter qu'il s'appuie sur une spécification plutôt... baroque et involontairement loufoque.
Si en revanche, vous souhaitez traiter le système historique, avec toutes ses particularités et toutes ses irrégularités, là c'est une autre paire de manches. Certains modules traitent de façon très partielle le système historique : le surlignement pour Text::Roman et Convert::Number::Roman et la graphie de type « (|) » pour Lingua::Romana::Perligata. J'ai eu l'intention d'écrire mon propre module de conversion, qui aurait traité l'ensemble des mécanismes décrits ci-dessus, mais j'y ai renoncé (temporairement ? :-). Pour paraphraser Douglas Adams lorsqu'il décrit les vaisseaux vogons, si la plupart des systèmes de numérations ont été conçus, élaborés et bâtis sur des principes rationnels, le système romain donne plutôt l'impression d'être le résultat d'une congélation.
Le texte et les images sont de Jean Forget, et disponibles sous licence Creative Commons paternité, pas de modification, sauf pour les images dont la paternité et la licence ont été explicitement precisées.
Et merci entre autres à Yves Agostini pour les photos qu'il m'a envoyées.